| Memory Capacity in GBytes |
Price in US dollars |
| 2 | $9.99 |
| 4 | $10.99 |
| 8 | $19.99 |
| 16 | $29.99 |
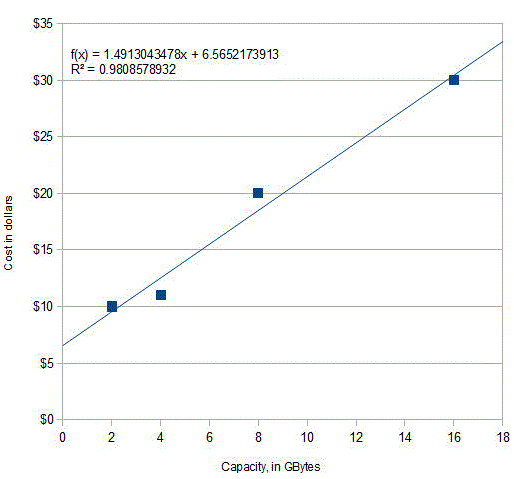 What's the
relationship between memory capacity and cost? Of course, we expect
that the larger-capacity cards should cost more than the
smaller-capacity ones, and if we plot cost vs capacity (graph on the
right), we can see a rough straight-line relationship. A
least-squares algorithm can compute the values of a
(intercept) and b (slope) of the straight line that is a
"best fit" to the data points. Using a linear least-squares
calculation, where X = capacity
and Y = cost, the
straight-line mathematical equation that most simply describes these
data (rounding to the nearest penny) is:
What's the
relationship between memory capacity and cost? Of course, we expect
that the larger-capacity cards should cost more than the
smaller-capacity ones, and if we plot cost vs capacity (graph on the
right), we can see a rough straight-line relationship. A
least-squares algorithm can compute the values of a
(intercept) and b (slope) of the straight line that is a
"best fit" to the data points. Using a linear least-squares
calculation, where X = capacity
and Y = cost, the
straight-line mathematical equation that most simply describes these
data (rounding to the nearest penny) is: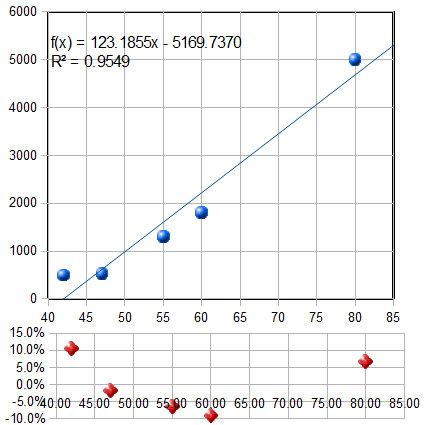 Here's
another related example: the historical prices of standard high
definition (not UHD) flat-screen LCD TVs as a function
of screen size, as advertised on the Web in the Spring of 2012.
The prices of five selected models, similar except for screen
size, are plotted against the screen size in inches in the
figure on the left, and are fit to a first-order (straight-line)
model. As for the previous example, the fit is not perfect. The
equation of the best-fit model is shown at the top of the graph,
along with the R2 value
(0.9549) indicating that the fit is not very good. And you can see
from the best-fit line that a 40 inch set would be predicted to have
a negative cost! They would pay you to take these
sets? I don't think so. Clearly something is wrong here.
Here's
another related example: the historical prices of standard high
definition (not UHD) flat-screen LCD TVs as a function
of screen size, as advertised on the Web in the Spring of 2012.
The prices of five selected models, similar except for screen
size, are plotted against the screen size in inches in the
figure on the left, and are fit to a first-order (straight-line)
model. As for the previous example, the fit is not perfect. The
equation of the best-fit model is shown at the top of the graph,
along with the R2 value
(0.9549) indicating that the fit is not very good. And you can see
from the best-fit line that a 40 inch set would be predicted to have
a negative cost! They would pay you to take these
sets? I don't think so. Clearly something is wrong here.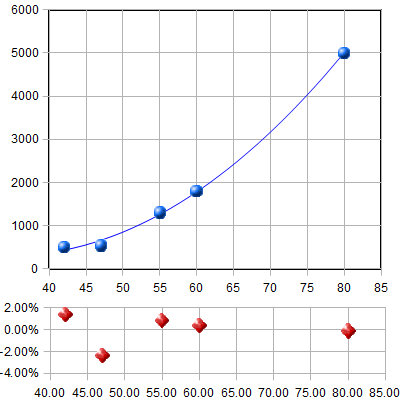

The graph on the
left shows a third example, taken from analytical chemistry:
a straight-line calibration data set where X = concentration
and Y = instrument reading (Y = a + bX). Click to download that data. The blue
dots are the data points. They don't all fall in a perfect
straight line because of random noise and measurement error in the
instrument readings and possibly also volumetric errors in
the concentrations of the standards (which are usually prepared in
the laboratory by diluting a stock solution). For this set of
data, the measured slope is 9.7926 and the intercept is 0.199. In
analytical chemistry, the slope of the calibration curve is often
called the "sensitivity". The intercept indicates the instrument
reading that would be expected if the concentration were zero.
Ordinarily instruments are adjusted ("zeroed") by the operator to
give a reading of zero for a concentration of zero, but random
noise and instrument drift can cause the intercept to be non-zero
for any particular calibration set. In this particular case, the
data are in fact computer-generated, and the "true" value of the
slope was exactly 10 and of the intercept was exactly zero before
noise was added, and the noise was added by a zero-centered
normally-distributed random-number generator. The presence of the
noise caused this particular measurement of slope to be off by
about 2%. (Had there been a larger number of points in this data
set, the calculated values of slope and intercept would almost
certainly have been better. On average, the accuracy of
measurements of slope and intercept improve with the square root of the number of points
in the data set). With this many data points, it's mathematically
possible to use an even higher polynomial degree, up to one
less that the number of data points, but it's not physically reasonable
in most cases; for example, you could fit a 9th
degree polynomial perfectly to these data, but the result is pretty wild. No
analytical instrument has a calibration curve that behaves like
that.
A plot
of the residuals for the calibration data (right) raises a
question. Except for the 6th data point (at a concentration of
0.6), the other points seem to form a rough U-shaped curve,
indicating that a quadratic equation might be a better model for
those points than a straight line. Can we reject the 6th point as
being an "outlier", perhaps caused by a mistake in preparing that
solution standard or in reading the instrument for that point?
Discarding that point would improve
the quality of fit (R2=0.992 instead of 0.986) especially if
a quadratic fit were used
(R2=0.998). The only way to know for sure is to repeat that
standard solution preparation and calibration and see if that U
shape persists in the residuals. Many instruments do give a very
linear calibration response, while others may show a slightly
non-linear response under some circumstances (for
example). But in fact, the calibration data used for this
particular example were computer-generated to be perfectly
linear, with normally-distributed random numbers added to
simulate noise. So actually that 6th point is really not an
outlier and the underlying data are not really curved, but you
would not know that in a real application. It would have
been a mistake to discard that 6th point and use a quadratic fit
in this case. Moral: don't throw out data points just because they
seem a little off, unless you have good reason, and don't use
higher-order polynomial fits just to get better fits if the
instrument is known to give linear response under those
circumstances. Even perfectly normally-distributed random errors
can occasionally give individual deviations that are quite far
from the average and might tempt you into thinking that they are
outliers. Don't be fooled. (Full disclosure: I obtained the
above example by "cherry-picking"
from among dozens of randomly generated data sets, in order to
find one that, although actually random, seemed to have an
outlier).
Solving the calibration equation for concentration. Once the calibration curve is established, it can be used to determine the concentrations of unknown samples that are measured on the same instrument, for example by solving the equation for concentration as a function of instrument reading. The result for the linear case is that the concentration of the sample Cx is given by Cx = (Sx - intercept)/slope, where Sx is the signal given by the sample solution, and "slope" and "intercept" are the results of the least-squares fit. If a quadratic fit is used, then you must use the more complex "quadratic equation" to solve for concentration, but the problem of solving the calibration equation for concentration becomes forbiddingly complex for higher order polynomial fits. (The concentration and the instrument readings can be recorded in any convenient units, as long as the same units are used for calibration and for the measurement of unknowns).

How reliable are the slope, intercept and other polynomial coefficients obtained from least-squares calculations on experimental data? The single most important factor is the appropriateness of the model chosen; it's critical that the model (e.g. linear, quadratic, gaussian, etc) be a good match to the actual underlying shape of the data. You can do that either by choosing a model based on the known and expected behavior of that system (like using a linear calibration model for an instrument that is known to give linear response under those conditions) or by choosing a model that always gives randomly-scattered residuals that do not exhibit a regular shape. But even with a perfect model, the least-squares procedure applied to repetitive sets of measurements will not give the same results every time because of random error (noise) in the data. If you were to repeat the entire set of measurements many times and do least-squares calculations on each data set, the standard deviations of the coefficients would vary directly with the standard deviation of the noise and inversely with the square root of the number of data points in each fit, all else being equal. The problem, obviously, is that it is not always possible to repeat the entire set of measurements many times. You may have only one set of measurements, and each experiment may be very expensive to repeat. So, it would be great if we had a short-cut method that would let us predict the standard deviations of the coefficients from a single measurement of the signal, without actually repeating the measurements.
Here I will describe three general ways to predict the standard deviations of the polynomial coefficients: algebraic propagation of errors, Monte Carlo simulation, and the bootstrap sampling method.
Algebraic
Propagation of errors. The classical way is based on the rules for
mathematical error propagation. The propagation of errors of the
entire curve-fitting method can be described in closed-form algebra by
breaking down the method into a series of simple differences,
sums, products, and ratios, and applying the rules for
error propagation to each step. The result of
this procedure for a first-order (straight line) least-squares fit
are shown in the last three lines of the set of equations in Math Details, below. Essentially, these
equations make use of the deviations from the least-squares line
(the "residuals") to estimate the standard deviations of the slope
and intercept, based on the assumption that the noise in that
single data set is random and is representative of the
noise that would be obtained upon repeated measurements. Because these predictions are based
only on a single data set, they are good only insofar as
that data set is typical of others that might be obtained
in repeated measurements. If your random errors happen to
be small when you acquire your data set, you'll get a
deceptively good-looking fit, but then your estimates of
the standard deviation of the slope and intercept will be too
low, on average. If your random errors happen to be large
in that data set, you'll get a deceptively bad-looking
fit, but then your estimates of the standard deviation will be too
high, on average. This problem becomes worse when the
number of data points is small. This is not to say that it is not
worth the trouble to calculate the predicted standard deviations
of slope and intercept, but keep in mind that these predictions
are accurate only if the number of data points is large (and only
if the noise is random and normally distributed). Beware: if the
deviations from linearity in your data set are systematic and
not random - for example, if try to fit a straight line to a smooth
curved data set - then the estimates the standard deviations
of the slope and intercept by these last two equations will be
too high, because they assume the deviations are caused by
random noise that varies from measurement to measurement, whereas
in fact a smooth curved data
set without random noise will give the same slope
and intercept from measurement to measurement.
The classical way is based on the rules for
mathematical error propagation. The propagation of errors of the
entire curve-fitting method can be described in closed-form algebra by
breaking down the method into a series of simple differences,
sums, products, and ratios, and applying the rules for
error propagation to each step. The result of
this procedure for a first-order (straight line) least-squares fit
are shown in the last three lines of the set of equations in Math Details, below. Essentially, these
equations make use of the deviations from the least-squares line
(the "residuals") to estimate the standard deviations of the slope
and intercept, based on the assumption that the noise in that
single data set is random and is representative of the
noise that would be obtained upon repeated measurements. Because these predictions are based
only on a single data set, they are good only insofar as
that data set is typical of others that might be obtained
in repeated measurements. If your random errors happen to
be small when you acquire your data set, you'll get a
deceptively good-looking fit, but then your estimates of
the standard deviation of the slope and intercept will be too
low, on average. If your random errors happen to be large
in that data set, you'll get a deceptively bad-looking
fit, but then your estimates of the standard deviation will be too
high, on average. This problem becomes worse when the
number of data points is small. This is not to say that it is not
worth the trouble to calculate the predicted standard deviations
of slope and intercept, but keep in mind that these predictions
are accurate only if the number of data points is large (and only
if the noise is random and normally distributed). Beware: if the
deviations from linearity in your data set are systematic and
not random - for example, if try to fit a straight line to a smooth
curved data set - then the estimates the standard deviations
of the slope and intercept by these last two equations will be
too high, because they assume the deviations are caused by
random noise that varies from measurement to measurement, whereas
in fact a smooth curved data
set without random noise will give the same slope
and intercept from measurement to measurement.
In the application to analytical calibration, the concentration of the sample Cx
is given by Cx = (Sx -
intercept)/slope, where Sx is the signal given by the
sample solution. The uncertainty of all three terms contribute
to the uncertainty of Cx. The standard deviation of Cx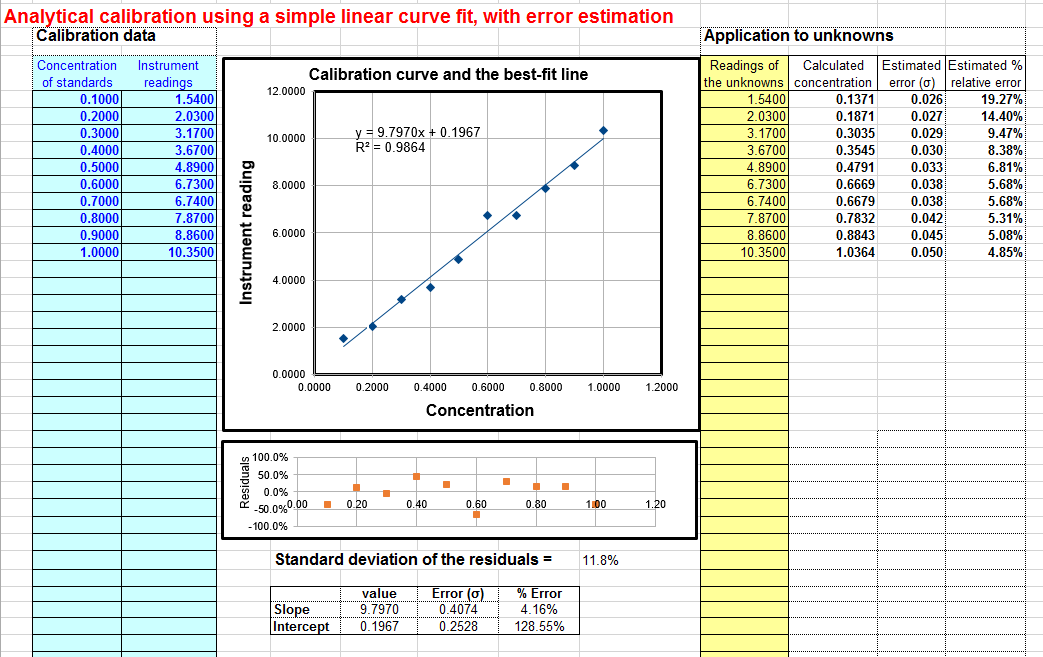 can be estimated from the standard
deviations of slope, intercept, and Sx using the
rules for mathematical
error propagation. But the problem is that, in
analytical chemistry, the labor and cost of preparing and running
large numbers of standards solution often limits the number of
standards to a rather small set, by statistical standards, so
these estimates of standard deviation are often fairly rough. A
spreadsheet that performs these error-propagation calculations for
your own first-order (linear) analytical calibration data can be
downloaded from http://terpconnect.umd.edu/~toh/models/CalibrationLinear.xls).
For example, the linear calibration example just given in the
previous section, where the "true" value of the slope was 10 and
the intercept was zero, this spreadsheet (whose screen shot shown
on the right) predicts that the slope is 9.8 with a standard
deviation 0.407 (4.2%) and that the intercept is 0.197 with a
standard deviation 0.25 (128%), both well within two standard
deviations of the true values. This spreadsheet also performs the
propagation of error calculations for the calculated
concentrations of each unknown in the last two columns on the
right. In the example in this figure, the instrument readings of
the standards are taken as the unknowns, showing that the
predicted percent concentration errors range from about 5% to 19%
of the true values of those standards. (Note that the standard
deviation of the concentration is greater at high concentrations
than the standard deviation of the slope, and considerably greater
at low concentrations because of the greater influence of the
uncertainly in the intercept). For a further discussion and some
examples, see "The
Calibration Curve Method with Linear Curve Fit". The
downloadable Matlab/Octave plotit.m
function uses the algebraic method to compute the standard
deviations of least-squares coefficients for any polynomial order.
can be estimated from the standard
deviations of slope, intercept, and Sx using the
rules for mathematical
error propagation. But the problem is that, in
analytical chemistry, the labor and cost of preparing and running
large numbers of standards solution often limits the number of
standards to a rather small set, by statistical standards, so
these estimates of standard deviation are often fairly rough. A
spreadsheet that performs these error-propagation calculations for
your own first-order (linear) analytical calibration data can be
downloaded from http://terpconnect.umd.edu/~toh/models/CalibrationLinear.xls).
For example, the linear calibration example just given in the
previous section, where the "true" value of the slope was 10 and
the intercept was zero, this spreadsheet (whose screen shot shown
on the right) predicts that the slope is 9.8 with a standard
deviation 0.407 (4.2%) and that the intercept is 0.197 with a
standard deviation 0.25 (128%), both well within two standard
deviations of the true values. This spreadsheet also performs the
propagation of error calculations for the calculated
concentrations of each unknown in the last two columns on the
right. In the example in this figure, the instrument readings of
the standards are taken as the unknowns, showing that the
predicted percent concentration errors range from about 5% to 19%
of the true values of those standards. (Note that the standard
deviation of the concentration is greater at high concentrations
than the standard deviation of the slope, and considerably greater
at low concentrations because of the greater influence of the
uncertainly in the intercept). For a further discussion and some
examples, see "The
Calibration Curve Method with Linear Curve Fit". The
downloadable Matlab/Octave plotit.m
function uses the algebraic method to compute the standard
deviations of least-squares coefficients for any polynomial order.
Monte Carlo simulation.  The second way of
estimating the standard deviations of the least-squares
coefficients is to perform a random-number simulation (a type of Monte
Carlo simulation). This requires that you know (by previous
measurements) the average standard deviation of the random noise
in the data. Using a computer, you construct a model of your data
over the normal range of X and Y values (e.g. Y = intercept
+ slope*X + noise,
where noise is the n
The second way of
estimating the standard deviations of the least-squares
coefficients is to perform a random-number simulation (a type of Monte
Carlo simulation). This requires that you know (by previous
measurements) the average standard deviation of the random noise
in the data. Using a computer, you construct a model of your data
over the normal range of X and Y values (e.g. Y = intercept
+ slope*X + noise,
where noise is the n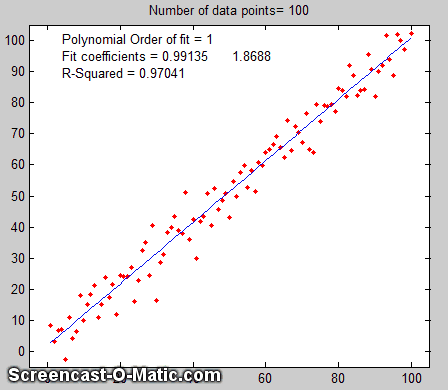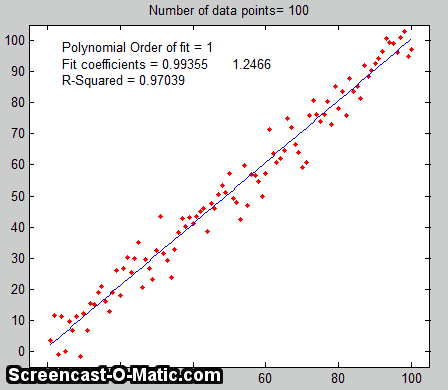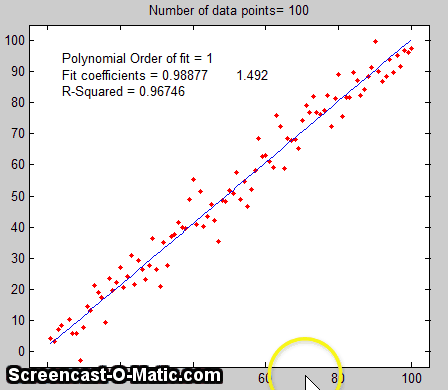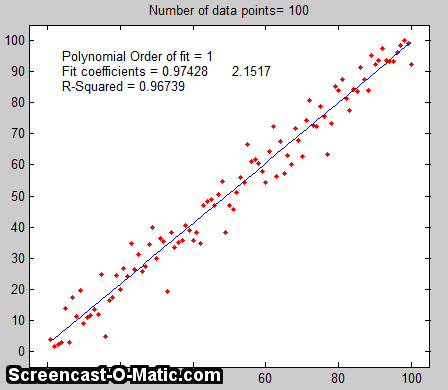 oise in the data), compute the
slope and intercept of each simulated noisy data set, then repeat
that process many times (usually a few thousand) with different
sets of random noise, and finally compute the standard deviation
of all the resulting slopes and intercepts. This is ordinarily
done with normally-distributed random noise (e.g. the RANDN
function that many programming languages have). These random
number generators produce "white" noise, but other noise colors can
be derived. If the model is good and the noise in the data
is well-characterized in terms of frequency distribution and
signal amplitude dependence, the results will be a very good
estimate of the expected standard deviations of the
least-squares coefficients. (If the noise is not constant, but
rather varies with the X or Y values, or if the noise is not white
or is not normally distributed, then that behavior must be
included in the simulation). An animated
example is shown on the right, for the case of a 100-point
straight line data set with slope=1, intercept=0, and standard
deviation of the added noise equal to 5% of the maximum value of
y. For each repeated set of simulated data, the fit coefficients
(least-squares measured slope and intercept) are slightly
different because of the noise.
oise in the data), compute the
slope and intercept of each simulated noisy data set, then repeat
that process many times (usually a few thousand) with different
sets of random noise, and finally compute the standard deviation
of all the resulting slopes and intercepts. This is ordinarily
done with normally-distributed random noise (e.g. the RANDN
function that many programming languages have). These random
number generators produce "white" noise, but other noise colors can
be derived. If the model is good and the noise in the data
is well-characterized in terms of frequency distribution and
signal amplitude dependence, the results will be a very good
estimate of the expected standard deviations of the
least-squares coefficients. (If the noise is not constant, but
rather varies with the X or Y values, or if the noise is not white
or is not normally distributed, then that behavior must be
included in the simulation). An animated
example is shown on the right, for the case of a 100-point
straight line data set with slope=1, intercept=0, and standard
deviation of the added noise equal to 5% of the maximum value of
y. For each repeated set of simulated data, the fit coefficients
(least-squares measured slope and intercept) are slightly
different because of the noise.
Obviously this method involves programming a computer to compute
the model and is not so convenient as evaluating a
simple algebraic expression. But there are two important
advantages to this method: (1) is has great generality; it can be
applied to curve fitting methods that are too complicated for the
classical closed-form algebraic propagation-of-error calculations,
even iterative non-linear methods;
and (2) its predictions are based on the average noise in the
data, not the noise in just a single data set. For that reason, it
gives more reliable estimations, particularly when the number of
data points in each data set is small. Nevertheless, you can
not always apply this method because you don't always know
the average standard deviation of the random noise in the
data. This type of computation is easily done in Matlab/Octave and
in spreadsheets.
You can download a MatlabOctave script that compares the Monte Carlo simulation to the algebraic method above from http://terpconnect.umd.edu/~toh/spectrum/LinearFiMC.m. By running this script with different sizes of data sets ("NumPoints" in line 10), you can see that the standard deviation predicted by the algebraic method fluctuates a lot from run to run when NumPoints is small (e.g. 10), but the Monte Carlo predictions are much more steady. When NumPoints is large (e.g. 1000), both methods agree very well.
The
Bootstrap.  The
third method is the "bootstrap"
method, a procedure that involves choosing random sub-samples
with replacement from a single data set and analyzing each sample
the same way (e.g. by a least-squares fit). Every sample is
returned to the data set after sampling, so that (a) a particular
data point from the original data set could appear multiple times
in a given sample, and (b) the number of elements in each
bootstrap sub-sample equals the number of elements in the original
data set. As a simple examp
The
third method is the "bootstrap"
method, a procedure that involves choosing random sub-samples
with replacement from a single data set and analyzing each sample
the same way (e.g. by a least-squares fit). Every sample is
returned to the data set after sampling, so that (a) a particular
data point from the original data set could appear multiple times
in a given sample, and (b) the number of elements in each
bootstrap sub-sample equals the number of elements in the original
data set. As a simple examp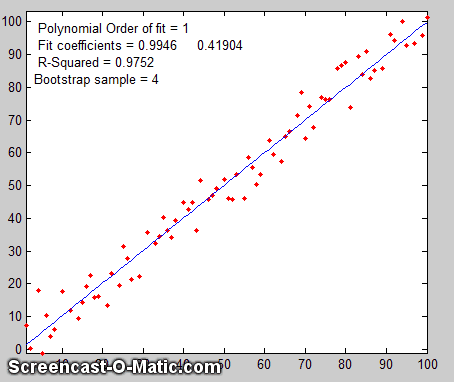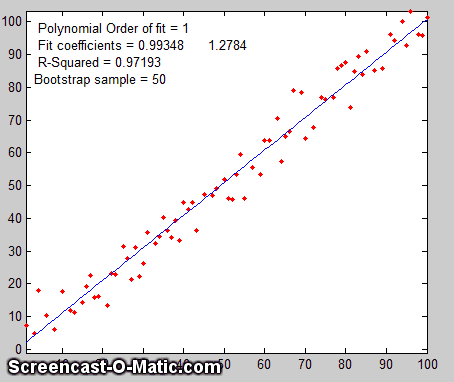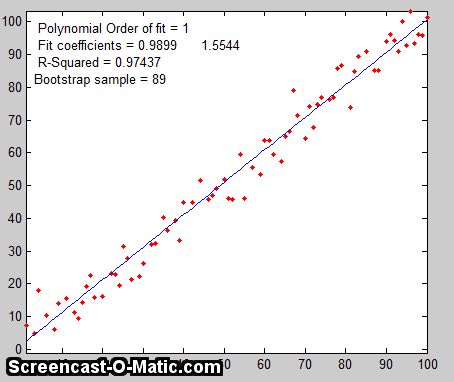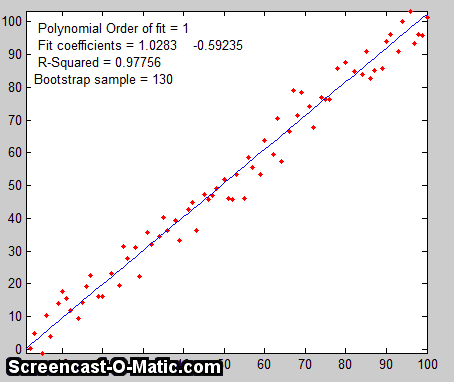 le, consider a data set with 10 x,y pairs
assigned the letters a
through j. The original
data set is represented as [a b
c d e f g h i j], and some typical bootstrap sub-samples
might be [a b b d e f f h i i]
or [a a c c e f g g i j],
each bootstrap sample containing the same number of data points,
but with about a third of the data pairs skipped, a third
duplicated, and a third left alone. (This is equivalent to
weighting a third of the data pairs by a factor of 2, a third by
0, and a third unweighted). You would use a computer to generate
hundreds or thousands of bootstrap samples like that and to apply
the calculation procedure under investigation (in this case a
linear least-squares) to each set.
le, consider a data set with 10 x,y pairs
assigned the letters a
through j. The original
data set is represented as [a b
c d e f g h i j], and some typical bootstrap sub-samples
might be [a b b d e f f h i i]
or [a a c c e f g g i j],
each bootstrap sample containing the same number of data points,
but with about a third of the data pairs skipped, a third
duplicated, and a third left alone. (This is equivalent to
weighting a third of the data pairs by a factor of 2, a third by
0, and a third unweighted). You would use a computer to generate
hundreds or thousands of bootstrap samples like that and to apply
the calculation procedure under investigation (in this case a
linear least-squares) to each set.
If there were no noise
in the data set, and if the model were properly chosen, then all
the points in the original data set and in all the bootstrap
sub-samples would fall exactly on the model line, with the result
that the least-squares results would be the same for every
sub-sample (click to
see an animation).
But if there is noise
in the data set, each set would give a slightly different result
(e.g. the least-squares polynomial coefficients), because
each sub-sample has a different subset of the random noise, as the
animation on the right demonstrates.
The process is illustrated by the animation on the right, for the same 100-point straight-line data set used above. (You can see that the variation in the fit coefficients between sub-samples is the same as for the Monte Carlo simulation above). The greater the amount of random noise in the data set, the greater would be the range of results from sample in the bootstrap set. This enables you to estimate the uncertainty of the quantity you are estimating, just as in the Monte-Carlo method above. The difference is that the Monte-Carlo method is based on the assumption that the noise is known, random, and can be accurately simulated by a random-number generator on a computer, whereas the bootstrap method uses the actual noise in the data set at hand, like the algebraic method, except that it does not need an algebraic solution of error propagation. The bootstrap method thus shares its generality with the Monte Carlo approach, but is limited by the assumption that the noise in that (possibly small) single data set is representative of the noise that would be obtained upon repeated measurements. The bootstrap method cannot, however, correctly estimate the parameter errors resulting from poor model selection. The method is examined in detail in its extensive literature. This type of bootstrap computation is easily done in Matlab/Octave and can also be done (with greater difficulty) in spreadsheets.
Comparison of error prediction methods. The Matlab/Octave script TestLinearFit.m
compares all three of these methods (Monte Carlo
simulation, the algebraic method, and the bootstrap method)
for a 100-point first-order linear least-squares fit. Each method
is repeated on different data sets with the same average slope,
intercept, and random noise, then the standard deviation (SD) of
the slopes (SDslope)
and intercepts (SDint)
were compiled and are tabulated below.
The Matlab/Octave script TestLinearFit.m
compares all three of these methods (Monte Carlo
simulation, the algebraic method, and the bootstrap method)
for a 100-point first-order linear least-squares fit. Each method
is repeated on different data sets with the same average slope,
intercept, and random noise, then the standard deviation (SD) of
the slopes (SDslope)
and intercepts (SDint)
were compiled and are tabulated below.
(You can download this script from http://terpconnect.umd.edu/~toh/spectrum/TestLinearFit.m).
On average, the mean standard deviation ("Mean SD") of the
three methods agree very well, but the algebraic and bootstrap
methods fluctuate more that the Monte Carlo simulation each time
this script is run, because they are based on the noise in one single 100-point data set,
whereas the Monte Carlo simulation reports the average of
many data sets. Of course, the algebraic method is simpler
and faster to compute than the other methods. However, an
algebraic propagation of errors solution is not always possible to
obtain, whereas the Monte Carlo and bootstrap methods do not
depend on an algebraic solution and can be applied readily to more
complicated curve-fitting situations, such as non-linear iterative least squares,
as will be seen later.
Effect of the number of data points on least-squares fit
precision. 
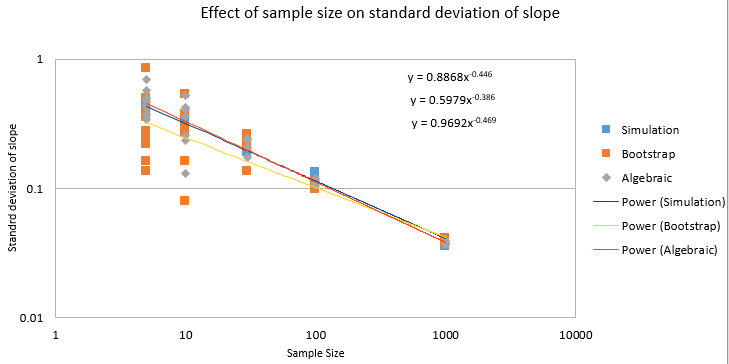 The spreadsheets EffectOfSampleSize.ods or
EffectOfSampleSize.xlsx,
which collect the results of many runs of TestLinearFit.m with different
numbers of data points ("NumPoints"), demonstrates that the
standard deviation of the slope and the intercept decrease if
the number of data points is increased; on average, the standard
deviations are inversely proportional to the square root of the
number of data points, which is consistent with the
observation that the slope of a log-log plot is roughly 1/2.
The spreadsheets EffectOfSampleSize.ods or
EffectOfSampleSize.xlsx,
which collect the results of many runs of TestLinearFit.m with different
numbers of data points ("NumPoints"), demonstrates that the
standard deviation of the slope and the intercept decrease if
the number of data points is increased; on average, the standard
deviations are inversely proportional to the square root of the
number of data points, which is consistent with the
observation that the slope of a log-log plot is roughly 1/2.
These plots really dramatize the problem of small sample sizes,
but this must be balanced against the cost of obtaining more data
points. For example, in analytical chemistry calibration, a larger
number of calibration points could be obtained either by preparing
and measuring more standard solutions or by reading each of a
smaller number of standards repeatedly. The former approach
accounts for both the volumetric errors in preparing solutions and
the random noise in the instrument readings, but the labor and
cost of preparing and running large numbers of standard solutions,
and safely disposing of them afterwards, is limiting. The latter
approach is less expensive but is less reliable because it
accounts only for the random noise in the instrument readings.
Overall, it better to refine the laboratory techniques and
instrument settings to minimize error that to attempts to
compensate by taking lots of readings.
It's very important that the
noisy signal not be smoothed
before the least-squares calculations, because doing so
will not improve the
reliability of the least-squares results, but it will cause both
the algebraic propagation-of-errors and the bootstrap calculations
to seriously underestimate the standard deviation of the
least-squares results. You can demonstrate using the most recent
version of the script TestLinearFit.m
by setting SmoothWidth in line 10 to something higher than 1,
which will smooth the data before the least-squares calculations.
This has no significant effect on the actual standard
deviation as calculated by the Monte Carlo method, but it
does significantly reduce the predicted standard
deviation calculated by the algebraic propagation-of-errors and
(especially) the bootstrap method. For similar reasons, if the
noise is pink rather
than white, the bootstrap error estimates will also be
low. Conversely, if the noise is blue, as occurs in
processed signals that have been subjected to some sort of differentiation process or that
have been deconvoluted from
some blurring process, then the errors predicted by the algebraic
propagation-of-errors and the bootstrap methods will be high.
(You can prove this to yourself by running TestLinearFit.m with pink and blue
noise modes selected in lines 23 and 24). Bottom line: error
prediction works best for white noise.

In some cases a fundamentally non-linear relationship can be transformed into a form that is amenable to polynomial curve fitting by means of a coordinate transformation (e.g. taking the log or the reciprocal of the data), and then least-squares method can be applied to the resulting linear equation. For example, the signal in the figure below is from a simulation of an exponential decay (X=time, Y=signal intensity) that has the mathematical form Y = a exp(bX), where a is the Y-value at X=0 and b is the decay constant. This is a fundamentally non-linear problem because Y is a non-linear function of the parameter b. However, by taking the natural log of both sides of the equation, we obtain ln(Y)=ln(a) + bX. In this equation, Y is a linear function of both parameters ln(a) and b, so it can be fit by the least squares method in order to estimate ln(a) and b, from which you get a by computing exp(ln(a)). In this particular example, the "true" values of the coefficients are a =1 and b = -0.9, but random noise has been added to each data point, with a standard deviation equal to 10% of the value of that data point, in order to simulate a typical experimental measurement in the laboratory. An estimate of the values of ln(a) and b, given only the noisy data points, can be determined by least-squares curve fitting of ln(Y) vs X.
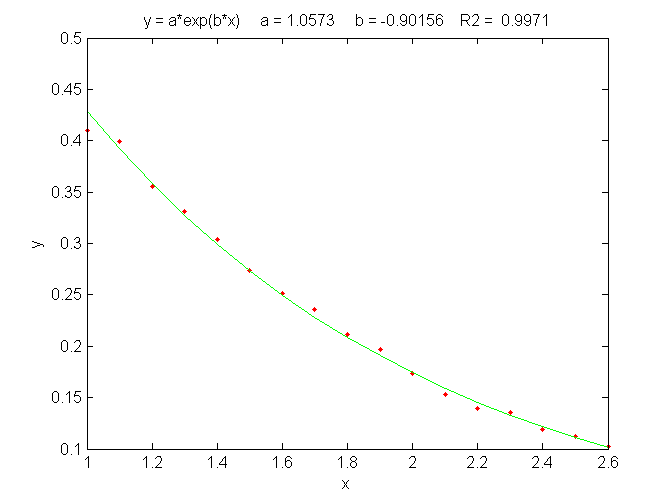
The best fit equation, shown by the green solid line in the
figure, is Y =0.959 exp(- 0.905 X), that is, a
= 0.959 and b = -0.905, which are reasonably close to
the expected values of 1 and -0.9, respectively. Thus, even in the
presence of substantial random noise (10% relative standard
deviation), it is possible to get reasonable estimates of the
parameters of the underlying equation (to within about 4%). The
most important requirement is that the model be good, that is,
that the equation selected for the model accurately describes the
underlying behavior of the system (except for noise). Often that
is the most difficult aspect, because the underlying models are
not always known with certainty. In Matlab and Octave, is
fit can be performed in a single line of code: polyfit(x,log(y),1),
which returns [b log(a)]. (In
Matlab and Octave, "log" is the natural log, "log10" is the
base-10 log).
Another example of the linearization of an exponential
relationship is explored in in Appendix R: Signal and Noise
in the Stock Market.
Other examples of non-linear relationships that can be linearized
by coordinate transformation include the logarithmic (Y = a
ln(bX)) and power (Y=aXb)
relationships. Methods of this type used to be very common back in
the days before computers, when fitting anything but a straight
line was difficult. It is still used today to extend the range of
functional relationships that can be handled by common linear
least-squares routines available in spreadsheets and hand-held
calculators. (The downloadable Matlab/Octave function trydatatrans.m tries eight different
simple data transformations on any given x,y data set and fits the
transformed data to a straight line or polynomial). Only a few
non-linear relationships can be handled by simple data
transformation, however. To fit any
arbitrary custom function, you may have to resort to the iterative
curve fitting method, which will be treated in Curve Fitting C.
Fitting
Gaussian and Lorentzian peaks.  An
interesting example of the use of transformation to convert a
non-linear relationship into a form that is amenable to
polynomial curve fitting is the use of the natural log (ln)
transformation to convert a positive Gaussian peak, which has the
fundamental functional form exp(-x2), into a parabola of the form -x2, which can be fit with a second order
polynomial (quadratic) function (y = a + bx + cx2). The equation for a Gaussian
peak is y = h*exp(-((x-p)./(1/(2*sqrt(ln(2)))*w)) ^2)), where h is
the peak height, p is the x-axis
location of the peak maximum, w is
the full width of the peak at half-maximum. The natural log of y
can
be shown to be log(h)-(4 p^2 log(2))/w^2+(8
p x log(2))/w^2-(4 x^2 log(2))/w^2,
which is a quadratic form in the independent variable x because
it is the sum of x^2, x, and constant terms. Expressing each of
the peak parameters h, p, and w in terms
of the three quadratic coefficients, a
little algebra (courtesy of Wolfram Alpha)
will show that all three parameters of the peak (height, maximum
position, and width) can be calculated from the three quadratic
coefficients a, b,
and c;
it's a classic "3 unknowns in 3 equations" problem. The peak
height is given by exp(a-c*(b/(2*c))^2),
the peak position by -b/(2*c), and the peak
half-width by 2.35482/(sqrt(2)*sqrt(-c)). This is called
"Caruana's Algorithm"; see Streamlining Digital
Signal Processing: A "Tricks of the Trade" Guidebook, Richard G. Lyons, ed., page 298.
The area under the Gaussian peak of height "height" and full
width at half maximum "width" can be shown to be
1.064467*height*width.
An
interesting example of the use of transformation to convert a
non-linear relationship into a form that is amenable to
polynomial curve fitting is the use of the natural log (ln)
transformation to convert a positive Gaussian peak, which has the
fundamental functional form exp(-x2), into a parabola of the form -x2, which can be fit with a second order
polynomial (quadratic) function (y = a + bx + cx2). The equation for a Gaussian
peak is y = h*exp(-((x-p)./(1/(2*sqrt(ln(2)))*w)) ^2)), where h is
the peak height, p is the x-axis
location of the peak maximum, w is
the full width of the peak at half-maximum. The natural log of y
can
be shown to be log(h)-(4 p^2 log(2))/w^2+(8
p x log(2))/w^2-(4 x^2 log(2))/w^2,
which is a quadratic form in the independent variable x because
it is the sum of x^2, x, and constant terms. Expressing each of
the peak parameters h, p, and w in terms
of the three quadratic coefficients, a
little algebra (courtesy of Wolfram Alpha)
will show that all three parameters of the peak (height, maximum
position, and width) can be calculated from the three quadratic
coefficients a, b,
and c;
it's a classic "3 unknowns in 3 equations" problem. The peak
height is given by exp(a-c*(b/(2*c))^2),
the peak position by -b/(2*c), and the peak
half-width by 2.35482/(sqrt(2)*sqrt(-c)). This is called
"Caruana's Algorithm"; see Streamlining Digital
Signal Processing: A "Tricks of the Trade" Guidebook, Richard G. Lyons, ed., page 298.
The area under the Gaussian peak of height "height" and full
width at half maximum "width" can be shown to be
1.064467*height*width.
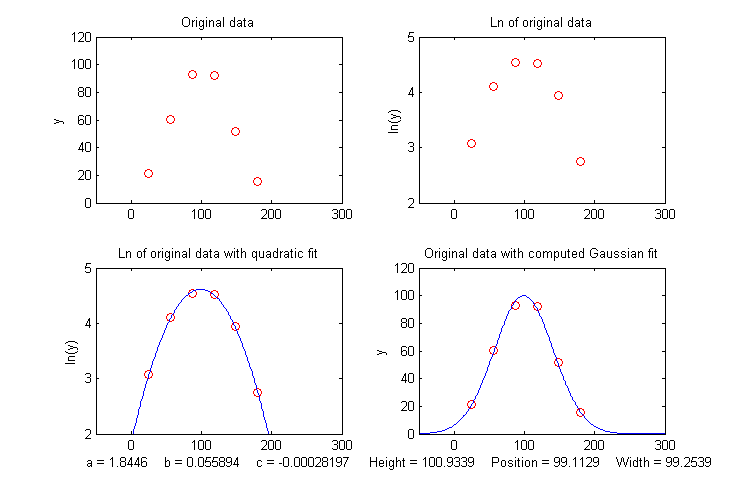 One advantage of this type of
Gaussian curve fitting, as opposed to simple visual estimation, is
illustrated in the figure on the left. The signal is a Gaussian
peak with a true peak height of 100 units, a true peak position of
100 units, and a true half-width of 100 units, but it is sparsely
sampled only every 31 units on the x-axis. The resulting data set, shown by
the red points in the upper left, has only 6 data points on the
peak itself. If we were to take the maximum of those 6
points (the 3rd point from the left, with x=87, y=95) as the peak
maximum, we'd get only a rough approximation to the true values of
peak position (100) and height (100). If we were to take the
distance between the 2nd the 5th data points as the peak width,
we'd get 3*31=93, compared to the true value of 100. If we were to
attempt to estimate the area under the peak from those
measurements, we would get 1.064467*95*93=9404.6, much lower than
the theoretical width of 1.064467*height*width=10644.67.
One advantage of this type of
Gaussian curve fitting, as opposed to simple visual estimation, is
illustrated in the figure on the left. The signal is a Gaussian
peak with a true peak height of 100 units, a true peak position of
100 units, and a true half-width of 100 units, but it is sparsely
sampled only every 31 units on the x-axis. The resulting data set, shown by
the red points in the upper left, has only 6 data points on the
peak itself. If we were to take the maximum of those 6
points (the 3rd point from the left, with x=87, y=95) as the peak
maximum, we'd get only a rough approximation to the true values of
peak position (100) and height (100). If we were to take the
distance between the 2nd the 5th data points as the peak width,
we'd get 3*31=93, compared to the true value of 100. If we were to
attempt to estimate the area under the peak from those
measurements, we would get 1.064467*95*93=9404.6, much lower than
the theoretical width of 1.064467*height*width=10644.67.
However, taking the natural log of the data (upper right) produces a parabola that can be fit with a quadratic least-squares fit (shown by the blue line in the lower left panel). From the three coefficients of the quadratic fit, we can calculate much more accurate values of the Gaussian peak parameters, shown at the bottom of the figure (height=100.93; position=99.11; width=99.25; area = 10663). The panel in the lower right shows the resulting Gaussian fit (in blue) displayed with the original data (red points). The accuracy of those peak parameters (about 1% in this example) is limited only by the noise in the data.
This figure was created in Matlab (or Octave), using this script. (The Matlab/Octave function gaussfit.m performs the calculation for an x,y data set. You can also download a spreadsheet that does the same calculation; it's available in OpenOffice Calc (Download link, Screen shot) and Excel formats). Note: in order for this method to work properly, the data set must not contain any zeros or negative points; if the signal-to-noise ratio is very poor, it may be useful to skip those points or to pre-smooth the data slightly to reduce this problem. Moreover, the original Gaussian peak signal must be a single isolated peak with a zero baseline, that is, must tend to zero far from the peak center. In practice, this means that any non-zero baseline must be subtracted from the data set before applying this method. (A more general approach to fitting Gaussian peaks, which works for data sets with zeros and negative numbers and also for data with multiple overlapping peaks, is the non-linear iterative curve fitting method, which will be treated later).
A similar method can be derived for a Lorentzian
peak, 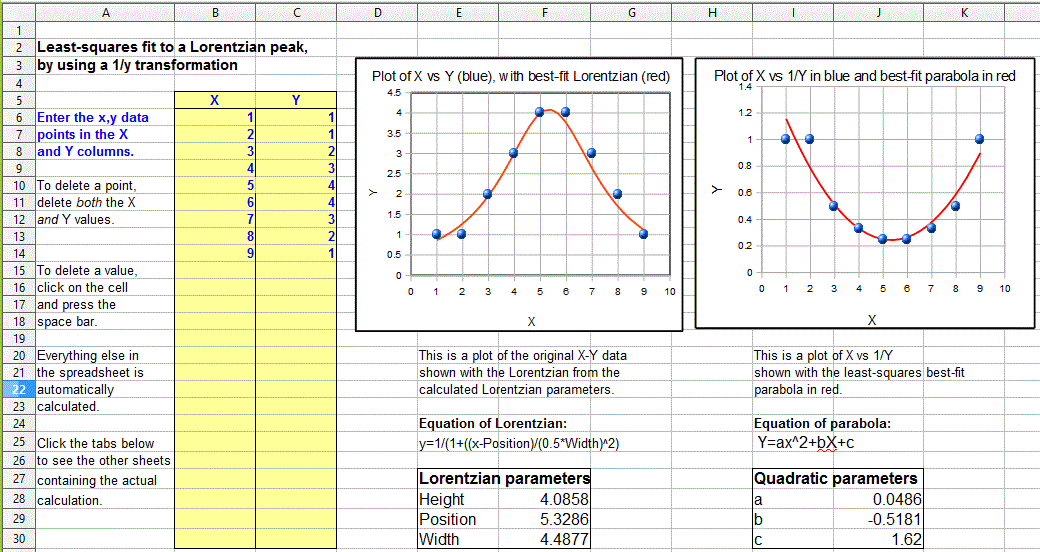 which has the fundamental form y=h/(1+((x-p)/(0.5*w))^2),
by fitting a quadratic to the reciprocal of y. As for
the Gaussian peak, all three parameters of the peak (height h,
maximum position p, and width w) can be calculated
from the three quadratic coefficients a, b, and c
of the quadratic fit: h=4*a/((4*a*c)-b^2), p=
-b/(2*a),
and
w= sqrt(((4*a*c)-b^2)/a)/sqrt(a).
Just as for the Gaussian case, the data set must not contain any
zero or negative y values. The Matlab/Octave function lorentzfit.m performs the calculation
for an x,y data set, and the Calc and Excel spreadsheets LorentzianLeastSquares.ods
and LorentzianLeastSquares.xls
perform the same calculation. (By the way, a quick way to test
either of the above methods is to use this simple peak data set: x=5,
20, 35 and y=5, 10, 5, which has a height, position, and width
equal to 10, 20, and 30, respectively, for a single isolated
symmetrical peak of any shape, assuming a baseline of zero).
which has the fundamental form y=h/(1+((x-p)/(0.5*w))^2),
by fitting a quadratic to the reciprocal of y. As for
the Gaussian peak, all three parameters of the peak (height h,
maximum position p, and width w) can be calculated
from the three quadratic coefficients a, b, and c
of the quadratic fit: h=4*a/((4*a*c)-b^2), p=
-b/(2*a),
and
w= sqrt(((4*a*c)-b^2)/a)/sqrt(a).
Just as for the Gaussian case, the data set must not contain any
zero or negative y values. The Matlab/Octave function lorentzfit.m performs the calculation
for an x,y data set, and the Calc and Excel spreadsheets LorentzianLeastSquares.ods
and LorentzianLeastSquares.xls
perform the same calculation. (By the way, a quick way to test
either of the above methods is to use this simple peak data set: x=5,
20, 35 and y=5, 10, 5, which has a height, position, and width
equal to 10, 20, and 30, respectively, for a single isolated
symmetrical peak of any shape, assuming a baseline of zero).
In order to apply the above methods to signals containing two
or more Gaussian or Lorentzian peaks, it's necessary to
locate all the peak maxima first, so that the proper groups of
points centered on each peak can be processed with the algorithms
just discussed. That is discussed in the section on Peak Finding and
Measurement.
But there is a downside to using coordinate transformation
methods to convert non-linear relationships into simple polynomial
form, and that is that the noise is also effected by the
transformation, with the result that the propagation
of error from the original data to the final results is
often difficult to predict. For example, in the method just
described for measuring the peak height, position, and width of
Gaussian or Lorentzian peaks, the results depends not only on the
amplitude of noise in the signal, but also on how many points
across the peak are taken for fitting. In particular, as you take
more points far from the peak center, where the y-values approach
zero, the natural log of those points approaches negative infinity
as y approaches zero. The result is that the noise of those
low-magnitude points is unduly magnified and has a disproportional
effect on the curve fitting. This runs counter the usual
expectation that the quality of the parameters derived from curve
fitting improves with the square root of the number of data points
(CurveFittingC.html#Noise).
A
reasonable compromise in this case is to take only the points
in the top half of the peak, with Y-values down to one-half
of the peak maximum. 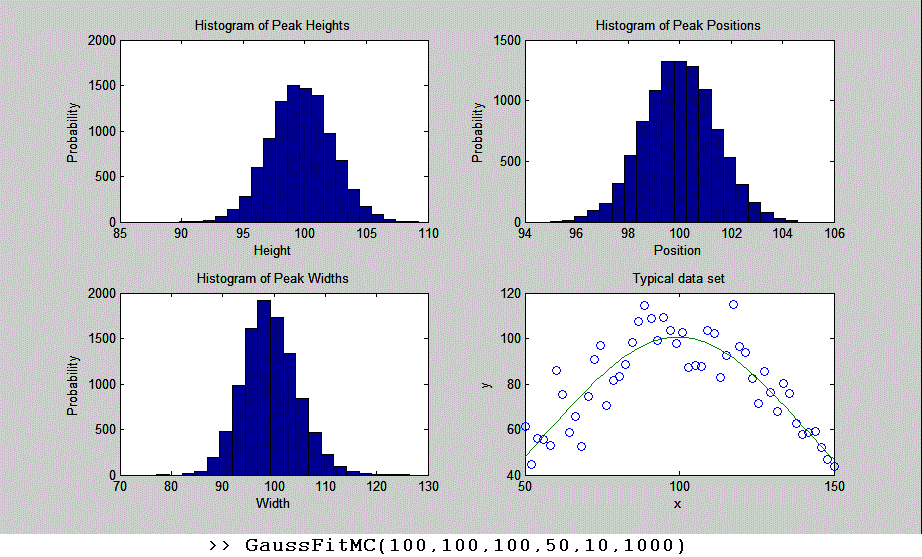 If you do that, the error propagation
(predicted by a Monte
Carlo simulation with constant normally-distributed random
noise) shows that the relative standard deviations of the measured
peak parameters are directly proportional to the noise in the data
and inversely
proportional to the square root of the number of data points (as
expected), but that the proportionality constants differ:
If you do that, the error propagation
(predicted by a Monte
Carlo simulation with constant normally-distributed random
noise) shows that the relative standard deviations of the measured
peak parameters are directly proportional to the noise in the data
and inversely
proportional to the square root of the number of data points (as
expected), but that the proportionality constants differ:
relative standard deviation of the peak height = 1.73*noise/sqrt(N),
relative standard deviation of the peak position = noise/sqrt(N),
relative standard deviation of the peak width = 3.62*noise/sqrt(N),
where noise is the standard deviation of the noise in the data and N in the number of data points taken for the least-squares fit. You can see from these results that the measurement of peak position is most precise, followed by the peak height, with the peak width being the least precise. If one were to include points far from the peak maximum, where the signal-to-noise ratio is very low, the results would be poorer than predicted. These predictions depend on knowledge of the noise in the signal; if only a single sample of that noise is available for measurement, there is no guarantee that sample is a representative sample, especially if the total number of points in the measured signal is small; the standard deviation of small samples is notoriously variable. Moreover, these predictions are based on a simulation with constant normally-distributed white noise; had the actual noise varied with signal level or with x-axis value, or if the probability distribution had been something other than normal, those predictions would not necessarily have been accurate. In such cases the bootstrap method has the advantage that it samples the actual noise in the signal.
You can download the Matlab/Octave code for this Monte Carlo simulation from GaussFitMC.m; view screen capture. A similar simulation (GaussFitMC2.m, view screen capture) compares this method to fitting the entire Gaussian peak with the iterative method in Curve Fitting 3, finding that the precision of the results are only slightly better with the (slower) iterative method.
Note 1: If you are reading this online, you can right-click on any of the m-file links above and select Save Link As... to download them to your computer for use within Matlab/Octave.
Note 2: In the curve
fitting techniques described here and in the next two sections,
there is no requirement that the x-axis interval between data
points be uniform, as is the assumption in many of the other
signal processing techniques previously covered. Curve
fitting algorithms typically accept a set of arbitrarily-spaced
x-axis values and a corresponding set of y-axis values.

The least-squares best fit for an x,y data set can be computed
using only basic arithmetic. Here are the relevant equations
for computing the slope and intercept of the first-order best-fit
equation, y = intercept + slope*x, as well as the predicted
standard deviation of the slope and intercept, and the coefficient
of determination, R2,
which is an indicator of the "goodness of fit". (R2 is 1.0000 if
the fit is perfect and less than that if the fit is imperfect).
| n = number of x,y data points sumx = Σx sumy = Σy sumxy = Σx*y sumx2 = Σx*x meanx = sumx / n meany = sumy / n slope = (n*sumxy - sumx*sumy) / (n*sumx2 - sumx*sumx) intercept = meany-(slope*meanx) ssy = Σ(y-meany)^2 ssr = Σ(y-intercept-slope*x)^2 R2 = 1-(ssr/ssy) Standard deviation of the slope = SQRT(ssr/(n-2))*SQRT(n/(n*sumx2 - sumx*sumx)) Standard deviation of the intercept = SQRT(ssr/(n-2))*SQRT(sumx2/(n*sumx2 - sumx*sumx)) |
(In these equations, Σ represents summation; for example, Σx
means the sum of all the x values, and Σx*y means the sum of all
the x*y products, etc).
The last two lines predict the standard deviation of the slope
and the intercept, based only on that data sample, assuming that
the deviations from the line are random and normally distributed.
These are estimates of the variability of slopes and intercepts
you are likely to get if you repeated the data measurements over
and over multiple times under the same conditions, assuming that
the deviations from the straight line are due to random
variability and not systematic error caused by
non-linearity. If the deviations are random, they will be slightly
different from time to time, causing the slope and intercept to
vary from measurement to measurement, with a standard deviation
predicted by these last two equations. However, if the deviations
are caused by systematic non-linearity, they will be the same from
from measurement to measurement, in which case the prediction of
these last two equations will not be relevant, and you might be
better off using a.polynomial fit such as a quadratic or cubic.
The reliability of these standard deviation estimates depends on
assumption of random deviations and also on the number of data
points in the curve fit; they improve with the square root of the
number of points. A slightly more
complex set of equations can be written to fit a
second-order (quadratic or parabolic) equations to a set of data;
instead of a slope and intercept, three coefficients are
calculated, a, b, and c, representing the
coefficients of the quadratic equation ax2+bx+c.
These calculations could be performed
step-by-step by hand, with the aid of a calculator or a
spreadsheet, with a program
written in any programming language, such as a Matlab or Octave script.

Spreadsheets
can perform the math described above easily; the spreadsheets pictured above (LeastSquares.xls and LeastSquares.odt for linear
fits and (QuadraticLeastSquares.xls and QuadraticLeastSquares.ods for quadratic fits), utilize the
expressions given above to compute and plot linear and quadratic
(parabolic) least-squares fit, respectively. The advantage of
spreadsheets is that they are highly customizable for your
particular application and can be deployed on mobile devices
such as tablets or smartphones. For straight-line fits, you can
use the convenient built-in functions slope and intercept.
The LINEST
function. Modern spreadsheets also have built-in
facilities for computing polynomial least-squares curve fits of any
order. For example, the LINEST function in both Excel
and OpenOffice
Calc can be used to compute polynomial and other curvilinear
least-squares fits. In addition to the best-fit polynomial
coefficients, the LINEST function also calculates at the same time
the standard error
values, the
determination coefficient (R2), the standard error value for
the y estimate, the F statistic, the
number of degrees of freedom,
the regression sum of squares, and the residual sum of
squares. A significant inconvenience of LINEST, compared to
working out the math using the series of mathematical expressions
described above, is that it is more difficult to adjust to a
variable number of data points and to remove suspect data points
or to change the order of the polynomial. LINEST is an array
function, which means that when you enter the formula in one
cell, multiple cells will be used for the output of the function.
You can't edit a LINEST function just like any other
spreadsheet function. To specify that LINEST is an array
function, do the following. Highlight the entire formula,
including the "=" sign. On the Macintosh, next, hold down the
"apple" key and press "return." On the PC hold down the "Ctrl" and
"Shift" keys and press "Enter." Excel adds "{ }" brackets around
the formula, to show that it is an array. Note that you cannot
type in the "{ }" characters yourself; if you do, Excel will treat
the cell contents as characters and not a formula. Highlighting
the full formula and typing the "apple" key or "Ctrl"+"Shift"
and "return" is the only way to enter an array formula. This
instruction sheet from Colby College gives step-by-step
instructions with screen shots.
Note: If you are working with a template that uses
the LINEST function, and you wish to change the number of data
points, the easiest way to do that is to select the rows or
columns containing the data, right-click on the row or column heading
(1,2,3 or a,b,c, etc), and then click Insert or Delete
in the right-click menu. If you do it that way, the LINEST
function referring to those rows or columns will be adjusted automatically.
That's easier than trying to edit the LINEST function directly.
(If you are inserting rows or columns, you must drag-copy the
formulas from the older rows or columns into the newly inserted
empty ones). See CalibrationCubic5Points.xls
for an example.
Application to analytical calibration and measurement using calibration curves.

There are specific
versions of these spreadsheets that apply curve fitting to calibration
curves (plots of signal measurements vs standards of known
concentration) and which also calculate the concentrations of
unknown samples (download complete set as CalibrationSpreadsheets.zip).
There are linear, quadratic, and cubic versions, as well versions
that perform a log-log conversion on the x and y data, apply
point-by-point weighting, and perform correction for sensor or
instrument drift. The linear
version computes the estimated standard deviations of the
slope and intercept and of the calculated concentrations of the
unknowns using the algebraic
method. One of the quadratic versions, CalibrationQuadraticB.xlsx,
computes the concentration standard deviation (column L)
and percent relative standard deviation (column M) using
the bootstrap method. In some cases, better overall results
can be obtained by weighting some calibration points more than
others, especially when the concentrations values cover a wide
range. There are weighted versions of the linear (CalibrationLinearWeighted.xls) and quadratic (CalibrationQuadraticWeighted.xls) templates, plus a quantitative comparison
of weighted and unweighted calibrations (graphic) for a test
case where the concentrations vary over a 1000-fold range. Of
course these spreadsheets can be used for just about any
measurement calibration application; just change the labels of the
columns and axes to match your particular application. A typical
application of these spreadsheet templates to pXRF (X-ray
fluorescence) analysis is shown in this YouTube video:
https://www.youtube.com/watch?v=U3kzgVz4HgQ
There is also another set
of spreadsheets that perform Monte
Carlo simulations of the calibration and measurement
process using several widely-used analytical calibration
methods, including first-order (straight line) and second order
(curved line) least squares fits. Typical systematic and random
errors in both signal and in volumetric measurements are
included, for the purpose of demonstrating how non-linearity,
interferences, and random errors combine to influence the final
result (the so-called "propagation of errors").


 quadratic fit. You must include
the output arguments, for example:
quadratic fit. You must include
the output arguments, for example:
It's important that the noisy
signal (x.y) not be smoothed if
the
bootstrap error predictions are to be accurate. Smoothing the data
will cause the bootstrap method to seriously underestimate the
precision of the results.
The gaussfit.m and lorentzfit.m functions are simple and easy but
they do not work well with very noisy peaks or for overlapping
peaks. As a demonstration, OverlappingPeaks.m
is a demo script that shows how to use gaussfit.m to measure two overlapping partially gaussian
peaks. It requires careful selection of the optimum
data regions around the top of each peak. Try changing the
relative position and height of the second peak or adding noise
(line 3) and see how it effects the accuracy. This function needs
the gaussian.m, gaussfit.m, and peakfit.m functions in the path.
The script also performs a measurement by the iterative method using peakfit.m,
which is more accurate but
takes about times longer to compute.
The downloadable Matlab-only functions iSignal.m
and ipf.m,
whose principal functions are fitting peaks, also have a
function for fitting polynomials of any order (Shift-o).
Recent versions of Matlab have a convenient tool for interactive manually-controlled (rather than programmed) polynomial curve fitting in the Figure window. Click for a video example: (external link to YouTube).
The Matlab Statistics Toolbox includes two types of bootstrap functions, "bootstrp" and "jackknife". To open the reference page in Matlab's help browser, type "doc bootstrp" or "doc jackknife".
